选修4-1:几何证明选讲
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP⊥OM于P.
(1)证明: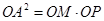 ;
;
(2)N为线段AP上一点,直线NB⊥ON且交圆O于B点,过B点的切线交直线ON于K.证明:∠OKM=90°.
选修4—4:坐标系与参数方程.
坐标系与参数方程在直角坐标系xOy中,圆C的参数方程 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)射线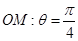 与圆C的交点为O、P两点,求P点的极坐标.
与圆C的交点为O、P两点,求P点的极坐标.
选修4—1:几何证明选讲.
已知圆内接△ABC中,D为BC上一点,且△ADC为正三角形,点E为BC的延长线上一点,AE为圆O的切线.
(Ⅰ)求∠BAE 的度数;
(Ⅱ)求证:
设函数
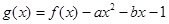 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)已知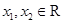 ,求证:
,求证: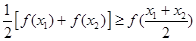 ;
;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
设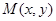 到定点
到定点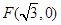 的距离和它到直线
的距离和它到直线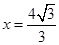 距离的比是
距离的比是 .
.
(Ⅰ)求点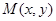 的轨迹方程;
的轨迹方程;
(Ⅱ) 为坐标原点,斜率为
为坐标原点,斜率为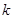 的直线过
的直线过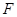 点,且与点
点,且与点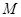 的轨迹交于点
的轨迹交于点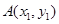 ,
,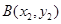 ,若
,若 ,求△
,求△ 的面积.
的面积.
在梯形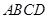 中,
中, ,
, ,
, ,
, ,如图把
,如图把 沿
沿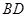 翻折,使得平面
翻折,使得平面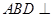 平面
平面 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若点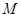 为线段
为线段 中点,求点
中点,求点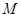 到平面
到平面 的距离.
的距离.