如图,空间四边形 中,
中,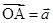 ,
, ,
, ,点
,点 在
在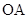 上,且
上,且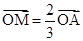 ,点
,点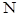 为
为 中点,则
中点,则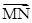 等于( )
等于( )
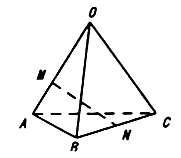
A. |
B.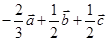 |
C.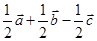 |
D.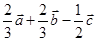 |
已知数列{an}是各项均为正数且公比不等于1的等比数列.对于函数y=f(x),若数列{lnf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的如下函数:
① ,
,
②f(x)=x2,
③f(x)=ex,
④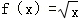 ,
,
则为“保比差数列函数”的所有序号为()
| A.①② | B.③④ | C.①②④ | D.②③④ |
对于各项均为整数的数列{an},如果ai+i(i=1,2,3,…)为完全平方数,则称数列{an}具有“P性质”,如果数列{an}不具有“P性质”,只要存在与{an}不是同一数列的{bn},且{bn}同时满足下面两个条件:①b1,b2,b3,…bn是a1,a2,a3,…,an的一个排列;②数列{bn}具有“P性质”,则称数列{an}具有“变换P性质”,下面三个数列:①数列1,2,3,4,5;②数列1,2,3,…,11,12;③数列{an}的前n项和为Sn= (n2﹣1).其中具有“P性质”或“变换P性质”的有()
(n2﹣1).其中具有“P性质”或“变换P性质”的有()
| A.③ | B.①③ | C.①② | D.①②③ |
设a>1,定义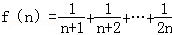 ,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是()
,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是()
A.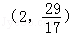 |
B.(0,1) | C.(0,4) | D.(1,+∞) |
《莱因德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给五个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,问最小1份为()
是较小的两份之和,问最小1份为()
A.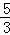 |
B.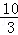 |
C. |
D.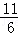 |
已知直线l经过点(﹣3,0)且与直线2x﹣y﹣3=0垂直,则直线l的方程为()
| A.x+2y+6=0 | B.x+2y+3=0 | C.2x+y+3=0 | D.2x+y+6=0 |