如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点，
，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示。
（Ⅰ）求出该几何体的体积；
（Ⅱ）试问在边
上是否存在点N，使
平面
？ 若存在，确定点N的位置(不需证明)；若不存在，请说明理由。
某教研机构准备举行一次高中数学新课程研讨会，拟邀请50名使用不同版本的一线教师参加，使用不同版本教材的教师人数如下表所示
(I)从这50名教师中随机选出2名教师发言，求第一位发言的教师所使用版本是北大师大版的概率；
(II)设使用北师大版的5名教师中有3名男教师，2名女教师，若随机选出2名用北师大版的教师发言，求抽到男教师个数的分布列和期望.
在ΔABC中，a，b, c分别是角A，B, C的对边，向量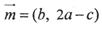
，
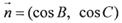，. 且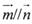
(I) 求角B的大小；
(II)设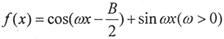
，且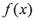
的最小正周期为
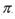，求
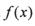在区间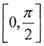
上的最大值和最小值.
已知函数 
，
．
(Ⅰ）当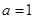 
时，求函数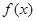 
的最小值；
(Ⅱ）当 
时，讨论函数 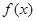的单调性；
已知椭圆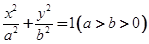
的左右焦点为F1，F2，离心率为
,以线段F1 F2为直径的圆的面积为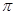
，
(1)求椭圆的方程；
(2) 设直线l过椭圆的右焦点F2（l不垂直坐标轴），且与椭圆交于A、B两点，线段AB的垂直平分线交x轴于点M（m,0），试求m的取值范围.
已知等差数列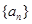
的各项均为正数，
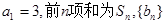是等比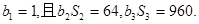数列，
求数列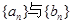
的通项公式；