已知各项均为正数的数列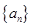 的前
的前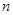 项和为
项和为 ,且对任意正整数
,且对任意正整数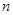 ,点
,点 都在直线
都在直线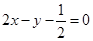 上.
上.
(1)求数列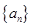 的通项公式;
的通项公式;
(2)若 设
设 求数列
求数列 前
前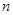 项和
项和 .
.
(本小题满分15分)已知二次函数 对
对 都满足
都满足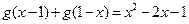 且
且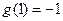 ,设函数
,设函数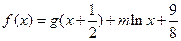
( ,
,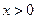 ).
).
(1)求 的表达式;
的表达式;
(2)若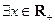 ,使
,使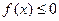
 成立,求实数
成立,求实数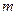 的取值范围;
的取值范围;
(3)设 ,
, ,求证:对于
,求证:对于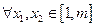 ,恒有
,恒有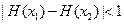 .
.
(本小题满分12分)已知函数f(x)=2x-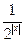 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
(本小题满分12分)已知△ABC的面积S满足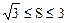 , 且
, 且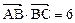 ,
, 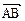 与
与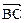 的夹角为
的夹角为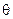 .
.
(I) 求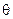 的取值范围;
的取值范围;
(II)求函数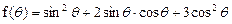 的最小值.
的最小值.
(本小题满分12分)等比数列{an}的各项均为正数,且2a1+3a2=1,a=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列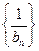 的前n项和.
的前n项和.
(本小题满分12分)数学试题中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的,评分标准规定:“每题只选1项,答对得5分,不答或答错得0分”,某考生每道题都给出了一个答案,已确定有6道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
(1)得50分的概率;
(2)得多少分的可能性最大?