如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设 (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
已知向量 ,
, ,设函数
,设函数 .
.
(1)求函数 的最大值;
的最大值;
(2)在锐角三角形 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且 的面积为3,
的面积为3, ,求
,求 的值.
的值.
某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
(Ⅰ)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人,求至多有
人,求至多有 人在分数段
人在分数段 的概率.
的概率.
已知 是实数,函数
是实数,函数 .
.
(Ⅰ)若 ,求
,求 的值及曲线
的值及曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间 上的最大值.
上的最大值.
在数列 中,a1=2, b1=4,且
中,a1=2, b1=4,且 成等差数
成等差数 列,
列,
 成等比数列(
成等比数列( )
)
(Ⅰ)求a2, a3, a4及b2, b3, b4,由此猜测{an}, {
{ bn}的通项公式,并证明你的结论;
bn}的通项公式,并证明你的结论;
(Ⅱ)证明: .
.
统计表明,某种型号的汽车在匀速行驶中每小时耗油量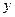 (升)关于行驶速度
(升)关于行驶速度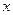 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: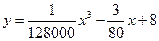
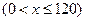 .已知甲、乙两地相距
.已知甲、乙两地相距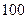 千米,当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
千米,当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?