已知椭圆 的中心在坐标原点,短轴长为4,且有一个焦点与抛物线
的中心在坐标原点,短轴长为4,且有一个焦点与抛物线 的焦点重合.
的焦点重合.
(1)求椭圆 的方程;
的方程;
(2)已知过定点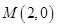 且斜率不为0的直线
且斜率不为0的直线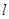 交椭圆
交椭圆 于
于 两点,试问在
两点,试问在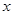 轴上是否存在一个定点
轴上是否存在一个定点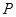 使得
使得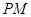 始终平分
始终平分 ?若存在,求出点
?若存在,求出点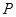 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
已知两圆x 2+y 2-2x-6y-1=0.x 2+y 2-10x-12y+m=0.
(1)m取何值时两圆外切?
(2)m取何值时两圆内切?
(3)当m=45时,求两圆的公共弦所在直线的方程和公共弦的长.
已知实数x,y满足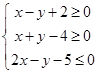
求:(1)z=x+2y-4的最大值;
(2)z=x2+y2-10y+25的最小值;
(3)z=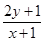 的取值范围.
的取值范围.
已知半径为5的圆的圆心在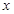 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线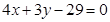 相切.
相切.
(1)求圆的方程;
(2)设直线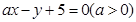 与圆相交于A,B两点,求实数
与圆相交于A,B两点,求实数 的取值范围.
的取值范围.
已知直线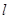 经过点A
经过点A ,求:
,求:
(1)直线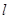 在两坐标轴上的截距相等的直线方程;
在两坐标轴上的截距相等的直线方程;
(2)直线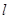 与两坐标轴的正半轴围成三角形面积最小时的直线方程.
与两坐标轴的正半轴围成三角形面积最小时的直线方程.
已知函数 ,
,
(1)求 在区间
在区间 的最小值
的最小值 ;(2)求
;(2)求 在区间
在区间 的值域
的值域