如图,在多面体 中,
中, 平面
平面 ,
, ,且
,且 是边长为
是边长为 的等边三角形,
的等边三角形, ,
, 与平面
与平面 所成角的正弦值为
所成角的正弦值为 .
.
(Ⅰ)若 是线段
是线段 的中点,证明:
的中点,证明: 面
面 ;
;
(Ⅱ)求二面角 的平面角的余弦值.
的平面角的余弦值.
(本小题满分12分)
已知二次函数 满足条件
满足条件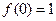 ,及
,及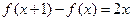 .
.
(1)求 的解析式;
的解析式;
(2)求 在
在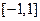 上的最值.
上的最值.
已知复数 (
( ),试问m为何值时,
),试问m为何值时,
(1)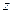 为实数?
为实数?
(2)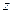 所对应的点落在第三象限?
所对应的点落在第三象限?


已知函数f(x)=x3+(m-4)x2-3mx+(n-6)对于定义域内的任意x,恒有f(-x)=-f(x)
(Ⅰ)求m、n的值
(Ⅱ)证明f(x)在区间(-2,2)上具有单调性
(Ⅲ)当-2≤x≤2时,(n-logm a)·logm a的值不大于f(x)的最小值,求实数a的取值范围。
近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是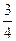 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是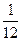 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是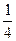 。
。
(Ⅰ)求乙、丙各自击中目标的概率。
(Ⅱ)求目标被击中的概率。