选修 :不等式选讲
:不等式选讲
设 .
.
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若存在实数 满足
满足 ,试求实数
,试求实数 的取值范围.
的取值范围.
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现 有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少?
某小组有男、女学生共13人,现从中选2人去完成一项任务。设每人当选的可能性相同。
⑴若选出的两人性别相同的概率为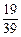 ,求选出的两人性别不同的概率;
,求选出的两人性别不同的概率;
⑵若已知该班男生有9人,求选出的两人性别不同的概率。
.已知两直线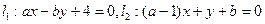 ,求满足下列条件的
,求满足下列条件的 、
、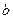 的值.直线
的值.直线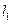 过点
过点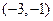 ,并且直线
,并且直线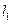 与直线
与直线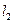 垂直;
垂直;
已知|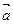 |=13,|
|=13,|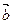 |=19,且|
|=19,且|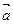 +
+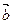 |=24,求|
|=24,求|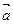 -
-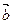 |的值
|的值
已知集合A =" {" x︱︱x-1︱>a,a>0 },集合B =" {" x︱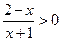 ,x∈R },若A∩B = Æ,试求实数a的取值范围.
,x∈R },若A∩B = Æ,试求实数a的取值范围.