定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M 成立,则称f(x)是D上的有界函数,其中M称为函f(x)的一个上界.已知函数f(x)=1+a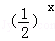 +
+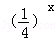 ,g(x)=
,g(x)=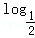
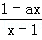 .
.
(1)若函数g(x)为奇函数,求实数a的值;
(2)在(1)的条件下,求函数g(x),在区间[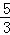 ,3]上的所有上界构成的集合;
,3]上的所有上界构成的集合;
(3)若函数f(x)在[0,+∞)上是以3为上界的有界函数,求实数a的取值范围.
已知 为正数,
为正数, ,且
,且 ,求证:
,求证: .
.
20世纪30年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级 ,其计算公式为
,其计算公式为 ,其中,
,其中, 是被测地震的最大振幅,
是被测地震的最大振幅, 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅
是20,此时标准地震的振幅是 ,计算这次地震的震级(精确到
,计算这次地震的震级(精确到 );
);
(2)5级地震给人的震感已比较明显,计算 级地震的最大振幅是5级地震
级地震的最大振幅是5级地震
的最大振幅的多少倍(精确到1).
已知函数 在区间
在区间 上恒为正值,
上恒为正值,
求实数 的取值范围.
的取值范围.
若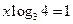 ,求
,求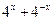 的值.
的值.
设 ,
, ,求证:
,求证:
(1) ;
;
(2) .
.