(本小题满分12分)若 ,且A∪B=A,求由实数a的值组成的集合。
,且A∪B=A,求由实数a的值组成的集合。
(本小题满分12分)求值:
(1) ;
;
(2)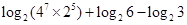 。
。
(本小题12分)如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ,该曲线段是函数
,该曲线段是函数 ,
,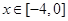 的图像,图像的最高点为
的图像,图像的最高点为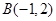 .边界的中间部分为长
.边界的中间部分为长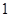 千米的直线段
千米的直线段 ,且
,且 .游乐场的后一部分边界是以
.游乐场的后一部分边界是以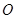 为圆心的一段圆弧
为圆心的一段圆弧 .
.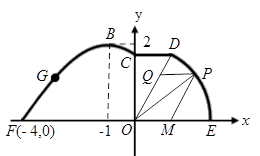
(1)求曲线段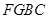 的函数表达式;
的函数表达式;
(2)曲线段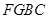 上的入口
上的入口 距海岸线
距海岸线 最近距离为
最近距离为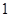 千米,现准备从入口
千米,现准备从入口 修一条笔直的景观路到
修一条笔直的景观路到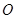 ,求景观路
,求景观路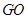 长;
长;
(3)如图,在扇形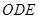 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区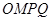 ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线 上,一边在半径
上,一边在半径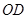 上,另外一个顶点
上,另外一个顶点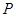 在圆弧
在圆弧 上,且
上,且 ,求平行四边形休闲区
,求平行四边形休闲区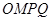 面积的最大值及此时
面积的最大值及此时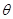 的值.
的值.
(本小题10分)在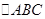 中,
中,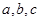 分别是角
分别是角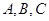 的对边,
的对边,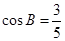 ,且
,且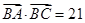 .
.
(Ⅰ)求 的值及
的值及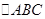 的面积;
的面积;
(Ⅱ)若 ,求角
,求角 的大小.
的大小.
(本小题12分)已知函数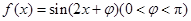 的图像经过点
的图像经过点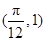 .
.
(1)求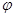 的值;
的值;
(2)在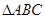 中,
中,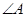 、
、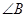 、
、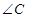 所对的边分别为
所对的边分别为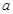 、
、 、
、 ,若
,若 ,且
,且 .求
.求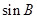 .
.