如图,半圆 的直径 ,以长为2的弦 为直径,向点 方向作半圆 ,其中 点在 上且不与 点重合,但 点可与 点重合.
发现: 的长与 的长之和为定值 ,求
思考:点 与 的最大距离为 ,此时点 , 间的距离为 ;
点 与 的最小距离为 ,此时半圆 的弧与 所围成的封闭图形面积为 ;
探究:当半圆 与 相切时,求 的长.
(注:结果保留 , ,

如图,在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯,实践证明:桌子边沿处的光的亮度与灯距离桌面的高度AO有关,且当sin∠ABO=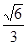 时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
时,桌子边沿处点B的光的亮度最大,设OB=60cm,求此时灯距离桌面的高度OA(结果精确到1cm).
(参考数据: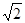 ≈1.414;
≈1.414;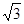 ≈1.732;
≈1.732;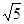 ≈2.236)
≈2.236)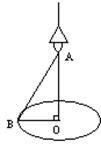
三明中学初三(1)班篮球队有10名队员,在一次投篮训练中,这10名队员各投篮50次的进球情况如下表:
| 进球数 |
42 |
32 |
26 |
20 |
19 |
18 |
15 |
14 |
| 人数 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
针对这次训练,请解答下列问题:
(1)求这10名队员进球数的平均数、中位数和众数;
(2)求这支球队整体投篮命中率;(投篮命中率= ×100%)
×100%)
(3)若队员小华的投篮命中率为40%,请你分析一下小华在这支球队中的投篮水平.
已知:关于x的方程x2+4x+a=0有两个实数根x1、x2,且2x1-x2=7,求实数a的值.
化简:(1+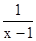 )÷
)÷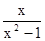 .
.
计算: -
- .
.