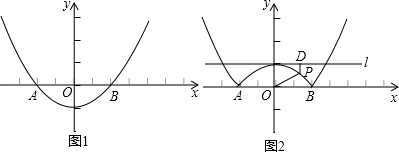
如图,抛物线 (常数 与 轴从左到右的交点为 , ,过线段 的中点 作 轴,交双曲线 于点 ,且 ,
(1)求 值;
(2)当 时,求 的长,并求直线 与 对称轴之间的距离;
(3)把 在直线 左侧部分的图象(含与直线 的交点)记为 ,用 表示图象 最高点的坐标;
(4)设 与双曲线有个交点的横坐标为 ,且满足 ,通过 位置随 变化的过程,直接写出 的取值范围.
在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.

解不等式组 ,并把解集在数轴上表示出来.
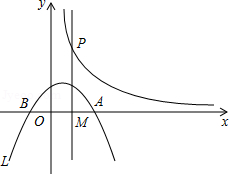
如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0).
(1)求抛物线的解析式;
(2)若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点P,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由.
(注:在解题过程中,如果你觉得有困难,可以阅读下面的材料)
附阅读材料:
1.在平面直角坐标系中,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则A,B两点间的距离为 ,这个公式叫两点间距离公式.
例如:已知A,B两点的坐标分别为(﹣1,2),(2,﹣2),则A,B两点间的距离为 .
2.因式分解:x4+2x2y2+y4=(x2+y2)2.
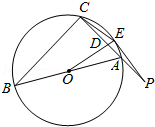
如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°, ,求证:DO=DP.