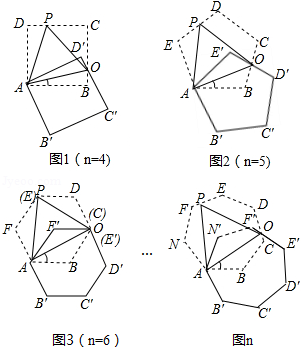
如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD="24" cm,BC="26" cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,四边形PQCD是等腰梯形?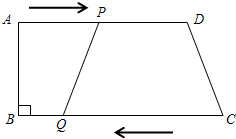
A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.
(1)求证:DH=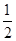 (AD+BC);
(AD+BC);
(2)若AC=6,求梯形ABCD的面积.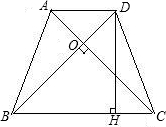
“立定跳远”是我市初中毕业生体育测试项目之一.测试时,记录下学生立定跳远的成绩,然后按照评分标准转化为相应的分数,满分10分.其中男生立定跳远的评分标准如下:注:成绩栏里的每个范围,含最低值,不含最高值.
| 成绩(米) |
… |
1.80~1.86 |
1.86~1.94 |
1.94~2.02 |
2.02~2.18 |
2.18~2.34 |
2.34~ |
| 得分 |
… |
5 |
6 |
7 |
8 |
9 |
10 |
某校九年级有480名男生参加立定跳远测试,现从中随机抽取10名男生测试成绩(单位:分)如下:
1.96 2.38 2.56 2.04 2.34 2.17 2.60 2.26 1.87 2.32
请完成下列问题:
(1)求这10名男生立定跳远成绩的极差和平均数;
(2)求这10名男生立定跳远得分的中位数和众数;
(3)如果将9分(含9分)以上定为“优秀”,请你估计这480名男生中得优秀的人数.
我国是一个严重缺水的国家,为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费,该市某户居民5月份用水x吨,应交水费y元.
(1)请写出y与x的函数关系式.
(2)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?