关于x的一元二次方程x2(2m1)xm210有两个不相等的实-优题课

题文

关于 $x$ 的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} - 1 = 0$ 有两个不相等的实数根．

（1）求 $m$ 的取值范围；

（2）写出一个满足条件的 $m$ 的值，并求此时方程的根．

科目数学题型解答题难度中等

知识点：解一元二次方程-因式分解法根的判别式

相关试题

如图，AB=AC,∠BAC=90⁰,BD⊥AE于D，CE⊥AE于E，且BD＞CE，求证:BD=EC+ED.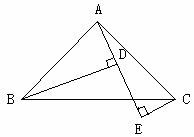

先化简再求代数式的值：
5a²＋[a ²＋（5a²－2a）－2（a ²－3a）]，其中；

解方程组：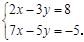

先观察图形，阅读相关文字后，再回答问题.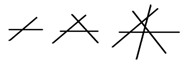

两条直线相交，最多有1个交点；
三条直线相交，最多有3个交点；
四条直线相交，最多有6个交点；
…… ……
问题：10条直线相交，最多有几个交点？

小张、小王、小李同时从湖边同一地点出发，绕湖行走．小张的速度是5.4千米/小时，小王的速度是4.2千米/小时，他们两人同向行走，小李与他们反向行走，半小时后小李和小张相遇，再经过5分钟，小李与小王相遇．那么绕湖一周的行程是多少千米？