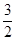已知 是 的函数,自变量 的取值范围 ,下表是 与 的几组对应值:
|
|
1 |
2 |
3 |
5 |
7 |
9 |
|
|
|
1.98 |
3.95 |
2.63 |
1.58 |
1.13 |
0.88 |
|
小腾根据学习函数的经验,利用上述表格所反映出的 与 之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系 中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
① 对应的函数值 约为 ;
②该函数的一条性质: .

平价商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.
(1)甲种商品每件进价为______元,每件乙种商品利润率为_____;
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件?
(3)在“元旦”期间,该商场只对甲乙两种商品进行如下的优惠促销活动:
| 打折前一次性购物总金额 |
优惠措施 |
| 不超过380元 |
不优惠 |
| 超过380元,但不超过500元 |
售价打九折 |
| 超过500元 |
售价打八折 |
按上述优惠条件,若小聪第一天只购买乙种商品,实际付款360元,第二天只购买甲种商品实际付款432元,求小聪这两天在该商场购买甲、乙两种商品一共多少件?
(如图,已知∠AOB=ll0°,∠AOC=m∠AOD,∠COE=n∠BOC,且3(m-2)+4=m+2,单项式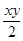 的系数为n.
的系数为n.
(1)求4(m-n) 2-(m-n) 2-5的值;
(2)当∠COD:∠COE=3:2时,试求∠COD的度数.
如图,点A、B.、C在同一条直线上,D为AC的中点,且AB=6cm,BC=2cm.
(1)试求AD的长;
(2)求AD:BD的值。
将一副三角尺按照如图的位置摆放,使得三角尺ACB的直角顶点C在三角尺DEF的直角边EF上.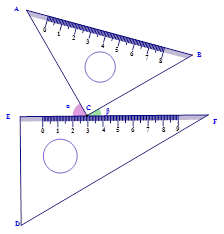
(1)求∠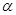 十∠
十∠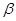 的度数;
的度数;
(2)若∠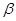 =32°,试问∠
=32°,试问∠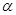 的补角为多少度?
的补角为多少度?
先化简后求值,2x-5(x-2y)+6x(1-3y),其中x=4,y=-