在等腰直角中,,是线段上一动点(与点、不重合),连接,延长至点,使得,过点作于点,交于点.
(1)若,求的大小(用含的式子表示).
(2)用等式表示线段与之间的数量关系,并证明.

如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.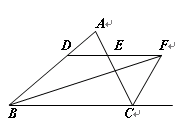
(1)试说明BD=DF;
(2)请写出图中所有的等腰三角形;
(3)线段BD,CE,DE之间存在怎样的数量关系?请说明理由.
如图,在等腰△ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F.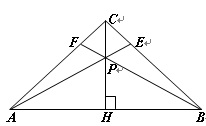
(1)试说明∠CAE=∠CBF;
(2)AE和BF 是否相等?请说明理由.
如图,已知AB∥CD,∠1=40º,∠2=70º,求出∠3,∠4的度数.
如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点.
(1)试说明BE=CD;
(2)请用一句话叙述由第(1)小题得出的结论.
如图,已知EF∥AD,∠1 =∠2,∠BAC=65º.请将求∠AGD的过程填写完整.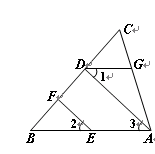
解:∵EF∥AD()
∴∠2= ()
又∵∠1=∠2
∴∠1=∠3()
∴AB∥ ()
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .