某年级共有300名学生.为了解该年级学生,两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.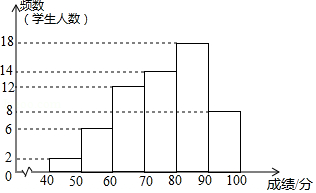
.课程成绩的频数分布直方图如下(数据分成6组:,,,,,
.课程成绩在这一组的是:70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
.,两门课程成绩的平均数、中位数、众数如下:
课程 |
平均数 |
中位数 |
众数 |
75.8 |
84.5 |
||
72.2 |
70 |
83 |
根据以上信息,回答下列问题:
(1)写出表中的值;
(2)在此次测试中,某学生的课程成绩为76分,课程成绩为71分,这名学生成绩排名更靠前的课程是 (填“”或“” ,理由是 ,
(3)假设该年级学生都参加此次测试,估计课程成绩超过75.8分的人数.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
有100米长的篱笆材料,想围成一个矩形露天仓库,要求面积不小于600平方米,在场地的北面有一堵长为50米的旧墙,有人用这个篱笆围成一个长40米,宽10米的矩形仓库,但面积只有400平方米,不合要求,现请你设计矩形仓库的长和宽,使它符合要求.
如图,某建筑工程队利用一面墙(墙的长度不限),用40米长的篱笆围成一个长方形的仓库.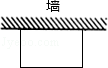
(1)求长方形的面积是150平方米,求出长方形两邻边的长;
(2)能否围成面积220平方米的长方形?请说明理由.
已知x1、x2是一元二次方程2x2﹣2x+m+1=0的两个实根.
(1)求实数m的取值范围;
(2)如果m满足不等式7+4x1x2>x12+x22,且m为整数.求m的值.
已知方程2(m+1)x2+4mx+3m=2,根据下列条件之一求m的值.
(1)方程有两个相等的实数根;
(2)方程有两个相反的实数根;
(3)方程的一个根为0.