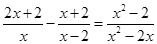为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸,在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 |
① |
② |
③ |
④ |
⑤ |
⑥ |
⑦ |
⑧ |
⑨ |
⑩ |
⑪ |
⑫ |
⑬ |
⑭ |
⑮ |
尺寸 |
8.72 |
8.88 |
8.92 |
8.93 |
8.94 |
8.96 |
8.97 |
8.98 |
9.03 |
9.04 |
9.06 |
9.07 |
9.08 |
按照生产标准,产品等次规定如下:
尺寸(单位: |
产品等次 |
特等品 |
|
优等品 |
|
合格品 |
|
或 |
非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格品个数时,将优等品(含特等品)计算在内.
(1)已知此次抽检的合格率为,请判断编号为⑮的产品是否为合格品,并说明理由.
(2)已知此次抽检出的优等品尺寸的中位数为.
求的值;
将这些优等品分成两组,一组尺寸大于,另一组尺寸不大于,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
一商场有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,某中学准备从甲、乙两种品牌的电脑中各选购一种型号的电脑安装到各班教室.
(1)写出所有选购方案(利用树状图或列表法表示);
(2)若(1)中各种选购方案被选中的可能性相同,那么A型号被选中的概率是多少?
(3)已知该中学用18万元人民币购买甲、乙两种品牌电脑刚好32台(价格如下表所示,单位:万元),其中甲品牌电脑选为A型号,求该中学购买到A型号电脑多少台?
| 品牌 |
甲 |
乙 |
|||
| 型号 |
A |
B |
C |
D |
E |
| 单价(万元) |
0.6 |
0.4 |
0.25 |
0.5 |
0.2 |
如图,当小华站立在镜子EF前A处时(镜子直立在地面上),他看自己的脚在镜中的像A1时的俯角为45°.若小华向后退0.5m到B处,这时他看自己的脚在镜中的像B1的俯角为30°.求小华的眼睛到地面的距离(结果精确到0.1m,参考数据 );
);
如图①表示的是某综合商场1-5月月销售额的情况,图②表示的是商场服装部1-5月月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
(1)来自商场财务部的数据报告表明,1-5月份商场销售总额一共是410万元,请你根据这一信息求商场4月份的销售额;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,商场服装部5月份的销售额比4月份减少了.你同意他的看法吗?请你说明理由.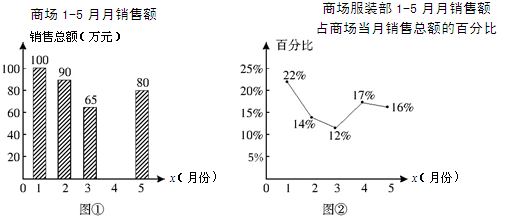
如图,在□ABCD中,E、F为BC上的两点,且BE=CF,AF=DE.
求证:(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
解方程: