如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着，，1，9，且任意相邻四个台阶上数的和都相等．
尝试 （1）求前4个台阶上数的和是多少？
（2）求第5个台阶上的数是多少？
应用 求从下到上前31个台阶上数的和．
发现 试用含为正整数）的式子表示出数“1”所在的台阶数．
如图: 在△AEB和△ADC中,给出以下四个论断：(1)AB=AC;(2)AD=AE;
(3)AM=AN;(4)AD⊥DC,AE⊥BE.以其中三个论断为题设,填入下面的“已知”栏中,一个论断为结论,填入下面的“求证”栏中，使之组成一个真命题，并写出证明过程。
如图，在△AEB和△ADC中，已知：＿＿＿＿＿＿＿＿＿＿＿＿＿＿.
求证: ＿＿＿＿＿＿＿.
证明:
在一个透明的袋子里，装有相同的四个小球，其上面分别标有数字－1，1，2，3.现从中任意摸出一个小球,将上面的数字作为点A的横坐标,不放回再从中摸出一个小球,将其上面的数字作为A点的纵坐标.用树状图或列表法写出A点坐标的所有可能性；
求点A在直线
上的概率；求点A的横坐标、纵坐标之和是偶数的概率.
如图:在直角坐标系中,线段OA=6cm，OA与y轴的夹角为30º.将线段OA绕原点按逆时针方向旋转到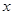
轴的负半轴上,得到线段OB.点A经过的路径是一条＿＿＿＿(填“线段”或“弧”),并求出此“路径”的长度；
求线段OA转到OB位置时，OA所“扫描” 过的图形的面积.
计算：
解不等式组：
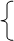
，并把解集在数轴上表示出来
如图，已知抛物线
与
轴交于A、B两点，与
轴交于点C．求A、B、C三点的坐标．
过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
在
轴上方的抛物线上是否存在一点M，过M作MG
轴于点G，使以A、M、G三点为顶点的三角形与
PCA相似．若存在，直接写出所有满足要求的M点的坐标；否则，请说明理由．