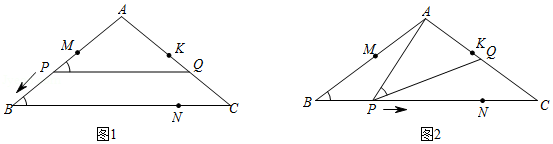
如图1和图2,在中,,,.点在边上,点,分别在,上,且.点从点出发沿折线匀速移动,到达点时停止;而点在边上随移动,且始终保持.
(1)当点在上时,求点与点的最短距离;
(2)若点在上,且将的面积分成上下两部分时,求的长;
(3)设点移动的路程为,当及时,分别求点到直线的距离(用含的式子表示);
(4)在点处设计并安装一扫描器,按定角扫描区域(含边界),扫描器随点从到再到共用时36秒.若,请直接写出点被扫描到的总时长.
如图,在平面直角坐标系中,△AOB的顶点坐标分别为A(2,1)、O(0,0)、B(1,-2).
(1)P(a,b)是△AOB的边AB上一点,△AOB经平移后点P的对应点为P2(a-3, b+1),请画出上述平移后的△A1O1B1,并写出点A1的坐标;
(2)以点O为位似中心,在y轴的右侧画出△AOB的一个位似△A2OB2,使它与△AOB的相似比为2:1,并分别写出点A、P的对应点A2、P2的坐标;
(3)判断△A2OB2与△A1O1B1能否是关于某一点Q为位似中心的位似图形,若是,请在图10中标出位似中心Q,并写出点Q的坐标.
如图,矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
已知关于x的方程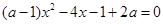 的一个根为
的一个根为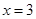 .
.
(1)求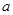 的值及方程的另一个根;
的值及方程的另一个根;
(2)如果一个三角形的三条边长都是这个方程的根,求这个三角形的周长.
解方程(每小题4分,共8分)
(1)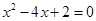 ;
;
(2)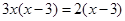 .
.
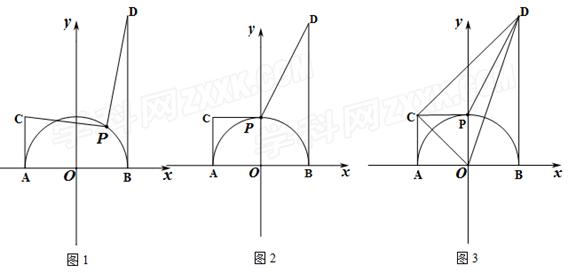
在平面直角坐标系xOy中,已知A(﹣2,0),B(2,0),AC⊥AB于点A,AC=2,BD⊥AB于点B,BD=6,以AB为直径的半圆O上有一动点P(不与A、B两点重合),连接PD、PC,我们把由五条线段AB、BD、DP、PC、CA所组成的封闭图形ABDPC叫做点P的关联图形,如图1所示.
(1)如图2,当P运动到半圆O与y轴的交点位置时,求点P的关联图形的面积.
(2)如图3,连接CD、OC、OD,判断△OCD的形状,并加以证明.
(3)当点P运动到什么位置时,点P的关联图形的面积最大,简要说明理由,并求面积的最大值.