如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.

根据以上信息,解答下列问题.
(1)冰冰同学所列方程中的表示 ,庆庆同学所列方程中的表示 ;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题.
某中学组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题: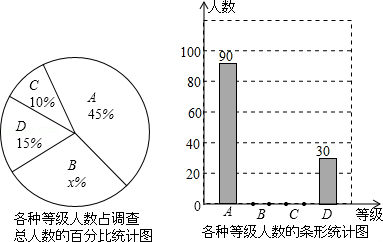
(1)本次随机抽取的学生人数为 人;
(2)求出x值,并将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读量满足2≤t<4的人数.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
如图,在正方形ABCD中,E、F分别为AB、BC上的点,且AE=BF,连结DE、AF,猜想DE、AF的关系并证明.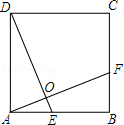
关于x的一元二次方程kx2﹣(2k﹣2)x+(k﹣2)=0(k≠0).
(1)求证:无论k取何值时,方程总有两个不相等的实数根.
(2)当k取何整数时方程有整数根.
一次函数y=kx+b(k≠0)的图象经过点(1,﹣3),且与y=2x平行,求这个一次函数表达式.