如图1,直线 交 轴于点 ,交 轴于点 ,抛物线 经过点 ,交 轴于点 .点 为抛物线上一个动点,过点 作 轴的垂线 ,过点 作 于点 ,连接 ,设点 的横坐标为 .
(1)求抛物线的解析式;
(2)当 为等腰直角三角形时,求线段 的长;
(3)如图2,将 绕点 逆时针旋转,得到△ ,且旋转角 ,当点 的对应点 落在坐标轴上时,请直接写出点 的坐标.

如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB=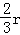 (r是⊙O的半径).
(r是⊙O的半径).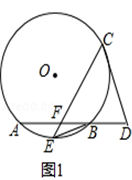
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)如图2,当F是AB的四等分点且EF·EC=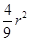 时,求EC的值.
时,求EC的值.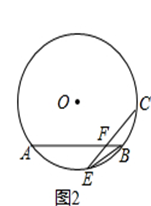
如图,已知⊙O上依次有A、B、C、D四个点,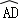 =
= ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.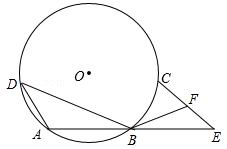
(1)若⊙O的半径为3,∠DAB=120°,求劣弧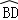 的长;
的长;
(2)求证:BF=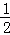 BD;
BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
如图,已知在△ABC中,AD是BC边上的中线,以AB为直径的⊙O交BC于点D,过D作MN⊥AC于点M,交AB的延长线于点N,过点B作BG⊥MN于G.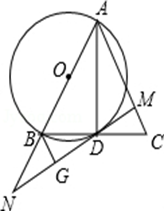
(1)求证:△BGD∽△DMA;
(2)求证:直线MN是⊙O的切线.
已知关于x的方程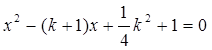 的两根是一个矩形两邻边的长.
的两根是一个矩形两邻边的长.
(1)k取何值时,方程在两个实数根;
(2)当矩形的对角线长为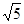 时,求k的值.
时,求k的值.
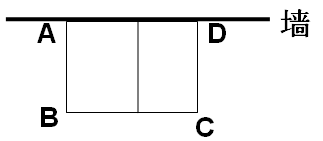
如图,要利用一面墙(墙长为25米)建羊圈,用75米的围栏围成总面积为300平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?