小明在研究矩形面积与矩形的边长,之间的关系时,得到下表数据:
0.5 |
1 |
1.5 |
2 |
3 |
4 |
6 |
12 |
|
12 |
6 |
4 |
3 |
2 |
|
1 |
0.5 |
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为 .
(2)与之间的函数关系式为 ,且随的增大而 .
(3)如图是小明画出的关于的函数图象,点、均在该函数的图象上,其中矩形的面积记为,矩形的面积记为,请判断和的大小关系,并说明理由.
(4)在(3)的条件下,交于点,反比例函数的图象经过点交于点,连接、,则四边形的面积为 .

如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.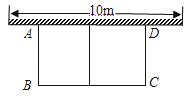
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
某商场将每件进价为80元的某种商品原来按每件100元出售,每天可售出100件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经过市场调查,发现这种商品售价每降低1元,商场销售量平均每天可增加10件,若商场经营该商品一天要获利润2160元,且让顾客得到实惠,则每件商品应降价多少元?
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.将△ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′′顺时针旋转90°,得到△A′′B′′C′′,请你画出△A′′B′′C′′和△A′′B′′C′′(不要求写画法).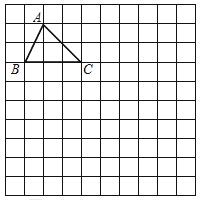
如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,求证:AC与⊙O相切.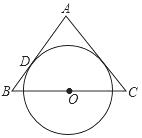
解下列一元二次方程.
(1)x2-5x+1=0;
(2)3(x-2)2=x(x-2).