如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为,双层部分的长度为,经测量,得到如下数据:
单层部分的长度 |
4 |
6 |
8 |
10 |
150 |
||
双层部分的长度 |
73 |
72 |
71 |
(1)根据表中数据的规律,完成以下表格,并直接写出关于的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为,求的取值范围.

如图,画一个两条直角边相等的Rt△ABC,并过斜边BC上一点D作射线AD,再分别过B、C作射线AD的垂线BE和CF,垂足分别为E、F,量出BE、CF、EF的长,改变D的位置,再重复上面的操作,你是否发现BE、CF、EF的长度之间有某种关系?能说清其中的奥妙吗?
已知如图,AC交BD于点O,AB=DC,∠A=∠D.(1)请写出符合上述条件的五个结论(并且不再添加辅助线,对顶角除外);(2)从你写出的5个结论中,任选一个加以证明.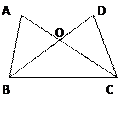
如图,AB=AC,∠BAC=900,BD⊥AE于D,CE⊥AE于E,且BD>CE,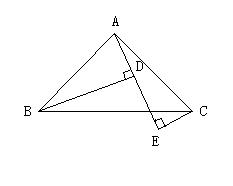 求证:BD=EC+ED.
求证:BD=EC+ED.
如图,AE是∠BAC的平分线,AB=AC。⑴若点D是AE上任意一点,则△ABD≌△ACD;⑵若点D是AE反向延长线上一点,结论还成立吗?试说明你的猜想。
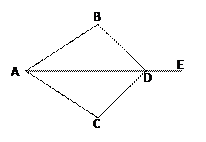 |
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28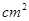 ,AB=20cm,AC=8cm,求DE的长。
,AB=20cm,AC=8cm,求DE的长。