问题提出
(1)如图①,是等边三角形,,若点是的内心,则的长为 ;
问题探究
(2)如图②,在矩形中,,,如果点是边上一点,且,那么边上是否存在一点,使得线段将矩形的面积平分?若存在,求出的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由草地和弦与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于(即每次喷灌时喷灌龙头由转到,然后再转回,这样往复喷灌.同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出,,的面积为;过弦的中点作交于点,又测得.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)

七年级十班为了表彰参加秋季运动会的队员,班主任特安排班长宋乐去商店买奖品,下面是宋乐与售货员的对话:
宋乐:阿姨,您好!
售货员:同学,你好,想买点什么?
宋乐:我只有100元,请帮我安排买10支钢笔和15本笔记本.
售货员:好,每支钢笔比每本笔记本贵2元,退你5元,请清点好,再见.
根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?
(第1小题满分4分,第2小题满分5分,本题满分共9分)
(1)已知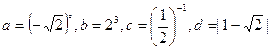 ,从
,从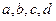 这4个数中任意选取3个数求和;
这4个数中任意选取3个数求和;
(2)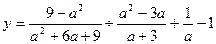 ,试说明在右边代数式有意义的条件下,不论
,试说明在右边代数式有意义的条件下,不论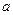 为
为
何值,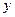 的值不变.
的值不变.
(本小题满分12分)
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.
(1)试问小球通过第二层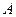 位置的概率是多少?
位置的概率是多少?
(2)请用学过的数学方法模拟试验,并具体说明小球下落到第三层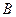 位置和第四层
位置和第四层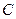
位置处的概率各是多少?
(本小题满分12分)
小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!
我只能将你最高翘到1米高,如果我俩各边的跷跷板都再伸长相同的一段长度,那么我
就能翘到1米25,甚至更高!”
(1)你认为小胖的话对吗?请你作图分析说明;
(2)你能否找出将小瘦翘到1米25高的方法?试说明.
(本小题满分10分)
已知二次函数图象经过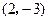 ,对称轴
,对称轴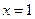 ,抛物线与
,抛物线与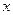 轴两交点距离为4,求这个二次函数的解析式?
轴两交点距离为4,求这个二次函数的解析式?