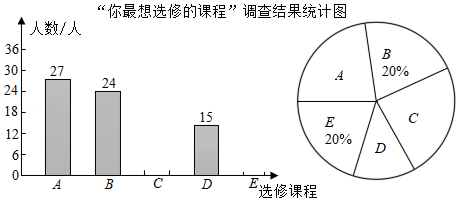
为了丰富学生的课余生活,满足学生个性化发展需求,某校计划在七年级开设选修课为了解学生选课情况,科学合理的配制资源,校教务处随机抽取了若干名七年级学生,对“你最想选修的课程”进行调查,可选修的课程有:(书法)、(航模)、(演讲与主持)、(足球)、(文学创作).经统计,被调查学生按学校的要求,并结合自己的喜好,每人都从这五门课程中选择了一门选修课.现将调查结果绘制成如图两幅不完整的统计图.
请根据以上提供的信息,解答下列问题:
(1)在这次调查中,课程(演讲与主持)的选修人数为 ,课程(文学创作)的选修人数为 ;
(2)在这次调查中,哪门课程的选修人数少于各门课程选修人数的平均数?
(3)若该校七年级有900名学生,请估计该年级想选修课程(航模)的学生人数.
(本题10分)如图,已知在⊙O中,直径AB为8cm,弦AC为4 cm,∠ACB的平分线交⊙O于D,连结BC,AD.(1)求BC的长.
(2)求∠CAD的度数
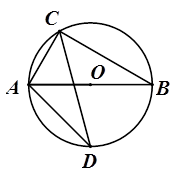
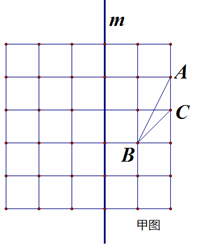
(本题10分) 如图,由边长为1的25个小正方形组成的正方形网格上有一个△ABC,请在网格上,按要求作出三角形,使它的三个顶点都落在小正方形的顶点上.(不要求写作法)(1)在甲图中作出△ABC关于直线m的轴对称图形.
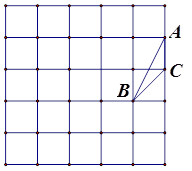
(2)在乙图中作一个和△ABC相似但不全等的△DEF,并直接写出△DEF的面积为.
(本题10分)在直角坐标平面内,二次函数图象的顶点为A(1,-4)且经过点B(3,0).(1)求该二次函数的解析式.
(2)求直线y=-x-1与该二次函数图象的交点的坐标.
(本题8分)广州亚运会期间某公司购买了亚运门票奖励给员工观看,门票种类、数量绘制的条形统计图如下图,下表为购买的三种比赛的门票价格.

依据上列图、表,回答下列问题:(1)其中观看跳水比赛的门票有张;观看乒乓球比赛的门票占全部门票的%;
(2)该公司决定采用随机抽取的方式把门票分配给100名员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀);在田径项目门票中有两张有刘翔参赛的项目,员工小亮抽到观看刘翔比赛的门票概率是;
(3)若这些门票的平均价格为84元,试求每张乒乓球门票的价格.
