如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形的圆心角为.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止).
(1)转动转盘一次,求转出的数字是的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

如图是小强洗漱时的侧面示意图,洗漱台(矩形 靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ,身体前倾成 ,脚与洗漱台距离 (点 , , , 在同一直线上).
(1)此时小强头部 点与地面 相距多少?
(2)小强希望他的头部 恰好在洗漱盆 的中点 的正上方,他应向前或后退多少?
, , ,结果精确到

小明为了了解气温对用电量的影响,对去年自己家的每月用电量和当地气温进行了统计.当地去年每月的平均气温如图1,小明家去年月用电量如图2.
根据统计图,回答下面的问题:

(1)当地去年月平均气温的最高值、最低值各为多少?相应月份的用电量各是多少?
(2)请简单描述月用电量与气温之间的关系;
(3)假设去年小明家用电量是所在社区家庭年用电量的中位数,据此他能否预测今年该社区的年用电量?请简要说明理由.
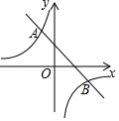
如图,一次函数 与反比例函数 的图象交于点 , .
(1)求这两个函数的表达式;
(2)在 轴上是否存在点 , ,使 为等腰三角形?若存在,求 的值;若不存在,说明理由.
如图,已知 , .
(1)在图中,用尺规作出 的内切圆 ,并标出 与边 , , 的切点 , , (保留痕迹,不必写作法);
(2)连接 , ,求 的度数.

如图,在平面直角坐标系 中,已知 , 两点的坐标分别为 , , 是线段 上一点(与 , 点不重合),抛物线 经过点 , ,顶点为 ,抛物线 经过点 , ,顶点为 , , 的延长线相交于点 .
(1)若 , ,求抛物线 , 的解析式;
(2)若 , ,求 的值;
(3)是否存在这样的实数 ,无论 取何值,直线 与 都不可能互相垂直?若存在,请直接写出 的两个不同的值;若不存在,请说明理由.
