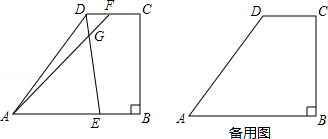
如图所示,梯形 中, , , , , ,点 是边 上的动点,点 是射线 上一点,射线 和射线 交于点 ,且 .
(1)求线段 的长;
(2)如果 是以 为腰的等腰三角形,求线段 的长;
(3)如果点 在边 上(不与点 、 重合),设 , ,求 关于 的函数解析式,并写出 的取值范围.
网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.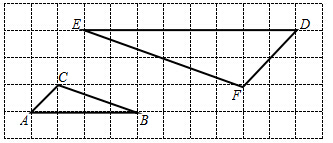
如图,抛物线经过A(-1,0),B(5,0),C(0,-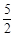 )三点.
)三点.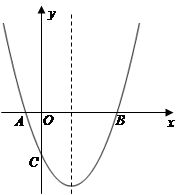
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.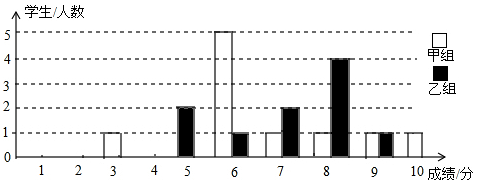
(1)补充完成下面的成绩统计分析表:
| 组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
| 甲组 |
6.7 |
3.41 |
90% |
20% |
|
| 乙组 |
7.5 |
1.69 |
80% |
10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.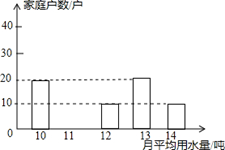
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
已知直线y=kx+6(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒2个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.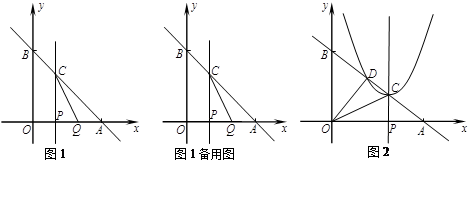
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当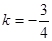 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长; ②设△COD的OC边上的高为h,当t为何值时,h的值最大?
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长; ②设△COD的OC边上的高为h,当t为何值时,h的值最大?