在平面直角坐标系xOy中（如图），已知抛物线yx22x，其顶-优题课

游客

题文

在平面直角坐标系 $xOy$ 中（如图），已知抛物线 $y = x^{2} - 2 x$ ，其顶点为 $A$ ．

（1）写出这条抛物线的开口方向、顶点 $A$ 的坐标，并说明它的变化情况；

（2）我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”．

①试求抛物线 $y = x^{2} - 2 x$ 的“不动点”的坐标；

②平移抛物线 $y = x^{2} - 2 x$ ，使所得新抛物线的顶点 $B$ 是该抛物线的“不动点”，其对称轴与 $x$ 轴交于点 $C$ ，且四边形 $OABC$ 是梯形，求新抛物线的表达式．

科目数学题型解答题难度中等

知识点：二次函数的性质二次函数图象与几何变换待定系数法求二次函数解析式二次函数综合题

登录免费查看答案和解析

相关试题

如图，⊙O的半径为l，等腰直角三角形ABC的顶点B的坐标为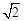（，0），∠CAB＝90°，AC＝AB，顶点A在⊙O上运动．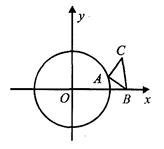

(1)当点A运动到x轴的负半轴上时，试判断直线BC与⊙O位置关系，并说明理由；
(2)当直线AB与⊙O相切时，求AB所在直线对应的函数关系式．

如图，已知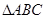中，D是AB中点，E是AC上的点，且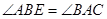，EF∥AB，DF∥BE，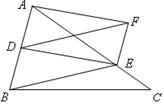

⑴猜想DF与AE有怎样的特殊关系？⑵证明你的猜想．

随着生活水平的提高，小林家购置了私家车，这样他乘坐私家车上学比乘坐公交车上学所需的时间少用了15分钟，现已知小林家距学校8千米，乘私家车平均速度是乘公交车平均速度的2.5倍，问乘公交车平均速度？

在一个不透明的袋子中装有3个除颜色外完全相同的小球，其中白球1个，黄球1个，红球1个，摸出一个球记下颜色后放回，再摸出一个球，请用列表或树形图法求两次都摸到红球的概率．

为了解学生课余活动情况，某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下面的问题：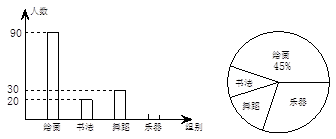

（1）此次共调查了多少名同学？
（2）将条形统计图补充完整，并计算扇形统计图中书法部分的圆心角的度数；
（3）如果该校共有名学生参加这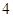个课外兴趣小组，而每位教师最多只能辅导本组的名学生，估计每个兴趣小组至少需要准备多少名教师．

试卷网试题网古诗词网作文网范文网