请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形的和两边上分别取一点和,使得.(如图)解决这个问题的操作步骤如下: 第一步,在上作出一点,使得,连接.第二步,在上取一点,作,交于点,并在上取一点,使.第三步,过点作,交于点.第四步,过点作,交于点,再过点作,交于点. 则有. 下面是该结论的部分证明: 证明:,, 又.△. . 同理可得.. ,.
|
任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成的证明过程;
(3)上述解决问题的过程中,通过作平行线把四边形放大得到四边形,从而确定了点,的位置,这里运用了下面一种图形的变化是 .
.平移 .旋转 .轴对称 .位似
如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
如图,射线PA切⊙O于点A,连接PO.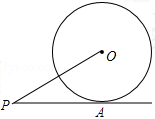
(1)在PO的上方作射线PC,使∠OPC=∠OPA(用尺规在原图中作,保留痕迹,不写作法),并证明:PC是⊙O的切线;
(2)在(1)的条件下,若PC切⊙O于点B,AB=AP=4,求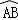 的长.
的长.
如图,反比例函数y= (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.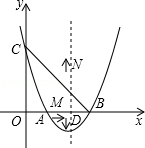
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.