观察下列各个等式的规律:
第一个等式:,第二个等式:,第三个等式:
请用上述等式反映出的规律解决下列问题:
(1)直接写出第四个等式;
(2)猜想第个等式(用的代数式表示),并证明你猜想的等式是正确的.
已知:如图,AB是⊙O的弦,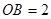 ,
,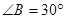 ,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.
,点C是弦AB上一动点(不与点A、B重合),连结CO并延长交⊙O于点D,连结AD.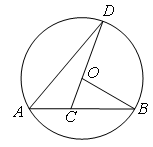
(1)求弦AB的长;
(2)当
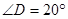 时,求
时,求 的度数;
的度数;(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、O、C为顶点的三角形相似?
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=6,试求BC、CD的长.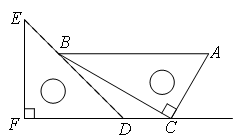
已知:反比例函数 (
( 且
且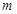 为正整数)的图象分布在第二、四象限,与一次函数
为正整数)的图象分布在第二、四象限,与一次函数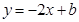 (b为常数)的图象相交于点
(b为常数)的图象相交于点 .试确定反比例函数和一次函数的解析式.
.试确定反比例函数和一次函数的解析式.
如图,AB为⊙O的弦,C、D分别是OA、OB延长线上的点,且CD∥AB,CD交⊙O于点E、F,若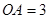 ,
, .
.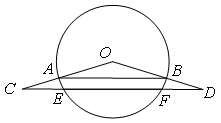
(1)求OD的长;
(2)若
 ,求弦EF的长.
,求弦EF的长.
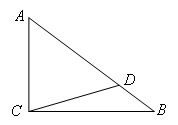
已知:如图,在Rt 中,
中, ,点D是斜边AB上的一点,且CD=AC=3,AB=4,求
,点D是斜边AB上的一点,且CD=AC=3,AB=4,求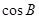 ,
, 及
及 的值.
的值.