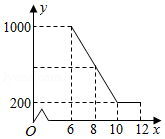
某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量(千克)与销售单价(元千克)的函数关系如图所示:
(1)求与的函数解析式(也称关系式);
(2)求这一天销售西瓜获得的利润的最大值.
如图,已知△ABC的三个顶点的坐标分别 为A(-6,0)、B(-2,3)、C(-1,0).
(1)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形;
(2)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
(每小题6分共12分)解方程
(1)2(x+2)2-8="0" ;
(2)2x2-7x+3=0.
如图,点E、D、F在同一条直线上,∠CDE=90°,∠1=∠2.
哪些角互为余角?哪些角互为补角?
∠ADC和∠BDC有什么关系?为什么?
∠ADF和∠BDE有什么关系?为什么?
解方程(每题4分,共8分)
(1)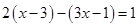
(2)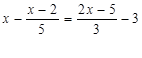
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地面: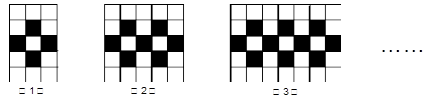
(1)观察图形,填写下表:
| 图形 |
(1) |
(2) |
(3) |
|
| 黑色瓷砖的块数 |
4 |
7 |
||
| 黑白两种瓷砖的总块数 |
15 |
25 |
(2)依上推测,第n个图形中黑色瓷砖的块数为;黑白两种瓷砖的总块数为(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2015块吗?若能,求出是第几个图形;若不能,请说明理由.