用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地面: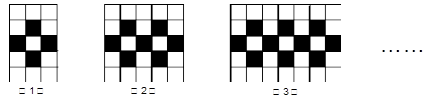
(1)观察图形,填写下表:
| 图形 |
(1) |
(2) |
(3) |
|
| 黑色瓷砖的块数 |
4 |
7 |
|
|
| 黑白两种瓷砖的总块数 |
15 |
25 |
|
|
(2)依上推测,第n个图形中黑色瓷砖的块数为 ;黑白两种瓷砖的总块数为 (都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2015块吗?若能,求出是第几个图形;若不能,请说明理由.
如图所示,点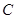 、
、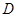 为线段
为线段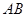 的三等分点,点
的三等分点,点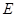 在线段
在线段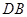 上,若
上,若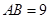 cm,
cm,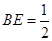 cm,求线段
cm,求线段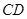 、
、 的长度.
的长度.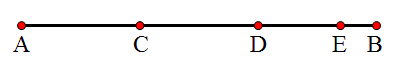
(本题满分14分 第(1)小题4分,第(2)小题4分,第(3)小题6分)
已知:如图,在△ABC中,AB=AC=15, cos∠A= .点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.
.点M在AB边上,AM=2MB,点P是边AC上的一个动点,设PA=x.
(1)求底边BC的长;
(2)若点O是BC的中点,联接MP、MO、OP,设四边形AMOP的面积是y,求y关于x的函数关系式,并出写出x的取值范围;
(3)把△MPA沿着直线MP翻折后得到△MPN,是否可能使△MPN的一条边(折痕边PM除外)与AC垂直?若存在,请求出x的值;若不存在,请说明理由.
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,二次函数 x2
x2  x
x  的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
的图像与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为Q,直线QB与y轴交于点E.
(1)求点E的坐标;
(2)在x轴上方找一点C,使以点C、O、B为顶点的三角形与△BOE相似,请直接写出点C的坐标.
(本题满分12分 第(1)小题6分,第(2)小题6分)
已知:如图,在△ABC中,BD⊥AC于点D, CE⊥AB于点E,EC和BD相交于点O,联接DE. 
(1)求证:△EOD∽△BOC;
(2)若S△EOD=16,S△BOC=36,求 的值.
的值.
已知:如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点M、N分别在边AO和边OD上,且AM= AO,ON=
AO,ON= OD,设
OD,设 =
= ,
, =
= ,试用
,试用 、
、 的线性组合表示向量
的线性组合表示向量 和向量
和向量 .
.