对任意一个三位数,如果满足各数位上的数字互不相同,且都不为零,那么称这个数为“相异数”.将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为.例如,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为,,所以.
(1)计算:,;
(2)若,都是“相异数”,其中,,,,都是正整数),规定:,当时,求的最大值.
观察下面方程的解法
x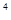 -13x
-13x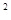 +36=0
+36=0
解:原方程可化为(x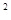 -4)(x
-4)(x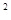 -9)=0
-9)=0
∴(x+2)(x-2)(x+3)(x-3)=0
∴x+2=0或x-2=0或x+3=0或x-3=0
∴x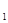 =2,x
=2,x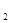 =-2,x
=-2,x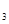 =3,x
=3,x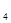 =-3
=-3
你能否求出方程x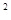 -3|x|+2=0的解?
-3|x|+2=0的解?
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.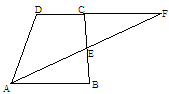
(1)求证:△ABE≌△FCE ;
(2)若BC⊥AB,且BC=16,AB=17,求AF的长.
计算:
计算:
如图1,已知双曲线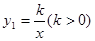 与直线
与直线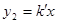 交于A,B两点,点A的坐标为(3,1).试解答下列问题:
交于A,B两点,点A的坐标为(3,1).试解答下列问题:

⑴求点B的坐标;
⑵当x满足什么范围时,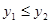 ;
;
⑶过原点O作另一条直线l,交双曲线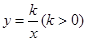 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.
①试判断四边形APBQ的形状,并加以说明;
② 若点P的横坐标为1,求四边形APBQ的面积;