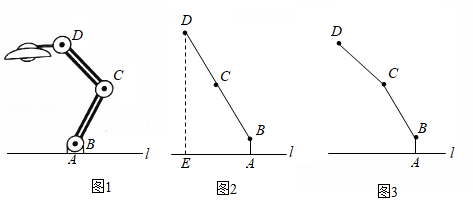
如图1为放置在水平桌面上的台灯,底座的高为,长度均为的连杆,与始终在同一平面上.
(1)转动连杆,,使成平角,,如图2,求连杆端点离桌面的高度.
(2)将(1)中的连杆再绕点逆时针旋转,使,如图3,问此时连杆端点离桌面的高度是增加还是减少?增加或减少了多少?(精确到,参考数据:,
解方程: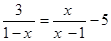 .
.
已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.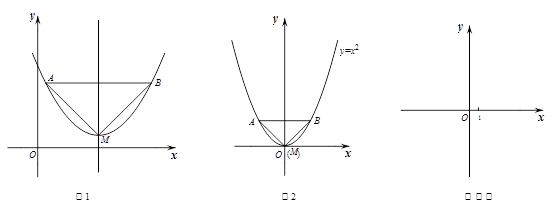
(1)①如图2,求出抛物线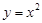 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线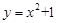 与
与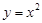 的“完美三角形”的斜边长的数量关系是;
的“完美三角形”的斜边长的数量关系是;
(2)若抛物线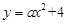 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线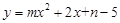 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且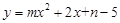 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.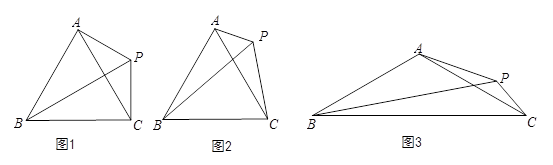
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.
在平面直角坐标系xOy中,抛物线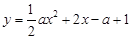 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为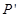 ,求点
,求点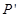 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(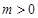 )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线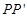 无交点,求m的取值范围.
无交点,求m的取值范围.
阅读、操作与探究:
小亮发现一种方法,可以借助某些直角三角形画矩形,使矩形邻边比的最简形式(如4:6的最简形式为2:3)为两个连续自然数的比,具体操作如下:
如图1,Rt△ABC中,BC,AC,AB的长分别为3,4,5,先以点B为圆心,线段BA的长为半径画弧,交CB的延长线于点D,再过D,A两点分别作AC,CD的平行线,交于点E.得到矩形ACDE,则矩形ACDE的邻边比为.
请仿照小亮的方法解决下列问题:
(1)如图2,已知Rt△FGH中,GH:GF:FH= 5:12:13,请你在图2中画一个矩形,使所画矩形邻边比的最简形式为两个连续自然数的比,并写出这个比值;
(2)若已知直角三角形的三边比为 (n为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为.
(n为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为.