某商店销售一种商品,每件的进价为50元,经市场调研发现,当该商品每件的售价为60元时,每天可销售200件;当售价高于进价时,每件的售价每增加1元,每天的销售数量将减少10件.
(1)当每件商品的售价为64元时,求该商品每天的销售数量;
(2)当每件商品的售价为多少时,销售该商品每天获得的利润最大?并求出最大利润.
(本题8分)
(1)计算: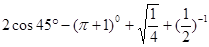 ;
;
(2)解不等式: ≤
≤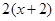
如图,在△ABC中,AB=5,AC=9,S△ABC= ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.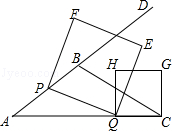
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,乐乐和颖颖相约到杭州市的某游乐园游玩,乐乐乘私家车从衢州出发1小时后,颖颖乘坐高铁从衢州出发,先到杭州火车站,然后再转车出租车取游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.
请结合图象解决下面问题:
(1)高铁的平均速度是每小时多少千米?
(2)当颖颖达到杭州火车东站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+3x﹣2的“旋转函数”.
小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;
(2)若函数y=﹣x2+ mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
(3)已知函数y=﹣ (x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣
(x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分布是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣ (x+1)(x﹣4)互为“旋转函数.”
(x+1)(x﹣4)互为“旋转函数.”
如图1,将矩形ABCD沿DE折叠,使顶点A落在DC上的点A′处,然后将矩形展平,沿EF折叠,使顶点A落在折痕DE上的点G处.再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.如图2.
(1)求证:EG=CH;
(2)已知AF= ,求AD和AB的长.
,求AD和AB的长.