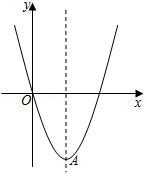
如图,在平面直角坐标系中,抛物线经过原点,顶点为.
(1)求抛物线的函数解析式;
(2)设点为抛物线的对称轴上的一点,点在该抛物线上,当四边
形为菱形时,求出点的坐标;
(3)在(2)的条件下,抛物线在第一象限的图象上是否存在一点,使得点到直线的距离与其到轴的距离相等?若存在,求出直线的函数解析式;若不存在,请说明理由.
三月份共付电费83.2元,按每家分电表的度数分摊电费。(请写出计算过程)
| 住户 |
分电表(度数) |
应付电费(元) |
| 王家 |
40 |
|
| 张家 |
38 |
|
| 赵家 |
29 |
|
| 李家 |
53 |
一项工程,甲独做10天完成,乙独做12天完成,现两人合做,完成后共得工资2200元,如果按完成工程量分配工资,甲、乙各分得多少元?
如图A点是中心广场所处的位置,B点是学校所处的位置,两地实际相距200m.
(1)量一量图上A、B两点的距离是_____cm,并把线段比例尺补充完整.
(2)图书馆在中心广场东偏南45°方向100m处,在图中用C表示出图书馆所在的位置.
(3)D点是王老师家所在的位置,学校在王老师家的_____方向,距王老师家实际有_____m.
已知抛物线m的顶点为(1,0),且经过点(0,1).
(1)求该抛物线对应的函数的解析式;
(2)将该抛物线向下平移m个单位,设得到的抛物线的顶点为A,与x轴的两个交点为B、C(点B在点C的左侧),若△ABC为等边三角形.
①求m的值;
②设点A关于x轴的对称点为点D,在抛物线上是否存在点P,使得以点P、C、B、D为顶点构成的四边形是菱形?若存在,请写出点P的坐标;若不存在,请说明理由.
如图1,是边长分别为6和4的两个等边三角形纸片ABC和CD1E1叠放在一起.
(1)操作:固定△ABC,将△CD1E1绕点C顺时针旋转得到△CDE,连接AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?并请说明理由;
(2)操作:固定△ABC,若将△CD1E1绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于点F,在线段CF上沿着CF方向平移,(点F与点P重合即停止平移)平移后的△CDE设为△PQR,如图3.
探究:在图3中,除三角形ABC和CDE外,还有哪个三角形是等腰三角形?写出你的结论(不必说明理由);
(3)探究:如图3,在(2)的条件下,设CQ=x,用x代数式表示出GH的长.