为了提高学生的阅读能力，我市某校开展了“读好书，助成长”的活动，并计划购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，请根据统计图回答下列问题：
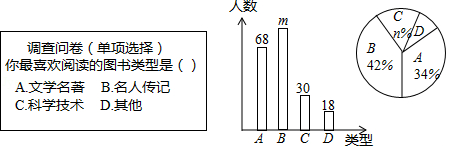
（1）本次调查共抽取了 名学生，两幅统计图中的 ， ．
（2）已知该校共有3600名学生，请你估计该校喜欢阅读“”类图书的学生约有多少人？
（3）学校将举办读书知识竞赛，九年级1班要在本班3名优胜者男1女）中随机选送2人参赛，请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率．
（本题7分）小明在学习三角形知识时，发现如下三个有趣的结论：在Rt△ABC中，∠A＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．
（1）如图①，M为边AC上一点，则BD、MF的位置关系是；
如图②，M为边AC反向延长线上一点，则BD、MF的位置关系是；
如图③，M为边AC延长线上一点，则BD、MF的位置关系是；
（2）请就图①、图②、或图③中的一种情况，给出证明．
（本题7分）阅读材料：
所以
=
，则 
=
=___________．
求（1）
（2）
．
作图题：（本题5分）如图，在△ABC中，∠BAC是钝角．
（1）画出边BC上的中线AD ；
（2）画出边BC上的高AH ；
（3）在所画图形中，共有个三角形，其中面积一定相等的三角形是．
先化简，再求值：（本题共2小题，每小题4分，共8分）
（1）
，其中
（2）
，其中
因式分解：（本题共2小题，每小题3分，共6分）
（1）
（2）