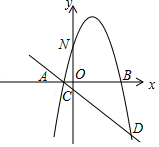
如图,抛物线与轴交于、两点在的左侧),与轴交于点,过点的直线与轴交于点,与抛物线的另一个交点为,已知,,点为抛物线上一动点(不与、重合).
(1)求抛物线和直线的解析式;
(2)当点在直线上方的抛物线上时,过点作轴交直线于点,作轴交直线于点,求的最大值;
(3)设为直线上的点,探究是否存在点,使得以点、,、为顶点的四边形为平行四边形?若存在,求出点的坐标;若不存在,请说明理由.
(本题5分)先化简,再求值: ,其中
,其中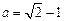 .
.
(本题4分)已知: ,求
,求 的值.
的值.
解下列关于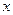 的方程:(每小题4分,共12分.)
的方程:(每小题4分,共12分.)
(1)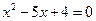 ;(2) x2-x-3=0
;(2) x2-x-3=0
(3)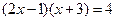
暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴ 张明他们一共去了几个成人,几个学生?
⑵ 请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?
说明理由。
⑶ 正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.
小黄做一道题“已知两个多项式A,B,计算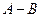 ”.小黄误将
”.小黄误将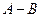 看作
看作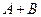 ,求得结果是
,求得结果是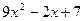 .若
.若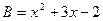 ,请你帮助小黄求出
,请你帮助小黄求出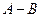 的正确答案.
的正确答案.