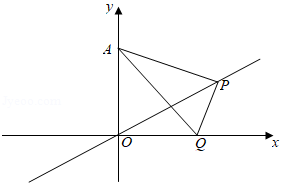
在平面直角坐标系中,已知,动点在的图象上运动(不与重合),连接.过点作,交轴于点,连接.
(1)求线段长度的取值范围;
(2)试问:点运动的过程中,是否为定值?如果是,求出该值;如果不是,请说明理由.
(3)当为等腰三角形时,求点的坐标.
根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如下(部分信息未给出):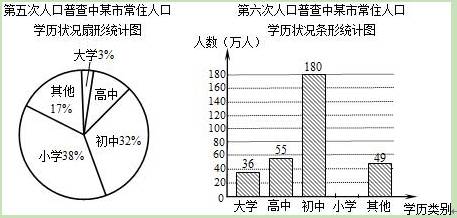
解答下列问题:
(1)计算第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)第六次人口普查结果与第五次相比,该市常住人口中高中学历人数增长的百分比是多少?
如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数 (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
解不等式组: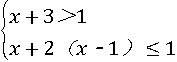 ,并把它的解在数轴上
,并把它的解在数轴上
表示出来.
(本小题10分)已知 抛物线
抛物线 :
: .点F(1,1).
.点F(1,1). (Ⅰ) 求抛物线
(Ⅰ) 求抛物线 的顶点坐标;
的顶点坐标;
(Ⅱ)
①若抛物线 与y轴的交点为A.连接AF,并延长交抛物线
与y轴的交点为A.连接AF,并延长交抛物线 于点B,求证:
于点B,求证:
②抛物线 上任意一点P(
上任意一点P( ))(
))( ).连接PF.并延长交抛物线
).连接PF.并延长交抛物线 于点Q(
于点Q( ),试判断
),试判断 是否成立?请说明理由;
是否成立?请说明理由;
(Ⅲ) 将抛物线 作适当的平移.得抛物线
作适当的平移.得抛物线 :
: ,若
,若 时.
时.

恒成立,求m的最大值.
(本小题10分)在平面直角坐标系中.已知O坐标原点.点A(3.0),B(0,4).以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转转角为α.∠ABO为β.
(I) 如图①,当旋转后点D恰好落在AB边上时.求点D的坐标;
(Ⅱ) 如图②,当旋转后满足BC∥x轴时.求α与β之闻的数量关系;
(Ⅲ) 当旋转后满足∠AOD=β时.求直线CD的解析式(直接写出即如果即可),