在矩形中,连结,点从点出发,以每秒1个单位的速度沿着的路径运动,运动时间为(秒.过点作于点,在矩形的内部作正方形.
(1)如图,当时,
①若点在的内部,连结、,求证:;
②当时,设正方形与的重叠部分面积为,求与的函数关系式;
(2)当,时,若直线将矩形的面积分成两部分,求的值.

在正方形网格图①、图②中各画一个等腰三角形.每个等腰三角形的一个顶点为
格点A,其余顶点从格点B、C、D、E、F、G、H中选取,并且所画的两个三角形不全等.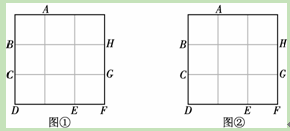
如图,平面直角坐标系中,直线 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线 在
在
第一象限内交于点B,BC⊥x轴于点C,OC=2AO.求双曲线的解析式.
平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋,其示意图如图所示.量
得角A为54°,斜边AB的长为2.1m,BC边上露出部分BD长为0.9m.求铁板BC边被掩
埋部分CD的长.(结果精确到0.1m)(参考数据:sin54°=0.81,cos54°=0.59,tan54°=1.38)
在长为10m,宽为8m的矩形空地上,沿平行于矩形各边的方向分割出三个全等
的小矩形花圃,其示意图如图所示.求其中一个小矩形花圃的长和宽.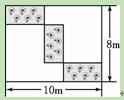
小华有3张卡片,小明有2张卡片,卡片上的数字如图所示.小华和小明分别从
自己的卡片中随机抽取一张.请用画树状图(或列表)的方法,求抽取的两张卡片上的数字
和为6的概率.