《中学生体质健康标准》规定的等级标准为:90分及以上为优秀,分为良好,分为及格,59分及以下为不及格.某校为了解七、八年级学生的体质健康情况,现从两年级中各随机抽取10名同学进行体质健康检测,并对成绩进行解析.成绩如下:
七年级 |
80 |
74 |
83 |
63 |
90 |
91 |
74 |
61 |
82 |
62 |
八年级 |
74 |
61 |
83 |
91 |
60 |
85 |
46 |
84 |
74 |
82 |
(1)根据上述数据,补充完成下列表格.
整理数据:
|
优秀 |
良好 |
及格 |
不及格 |
七年级 |
2 |
3 |
5 |
0 |
八年级 |
1 |
4 |
4 |
1 |
解析数据:
年级 |
平均数 |
众数 |
中位数 |
七年级 |
76 |
74 |
77 |
八年级 |
|
74 |
|
(2)该校目前七年级有200人,八年级有300人,试估计两个年级体质健康等级达到优秀的学生共有多少人?
(3)结合上述数据信息,你认为哪个年级学生的体质健康情况更好,并说明理由.
先化简,再求值: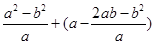 ,其中
,其中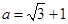 ,
,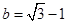 .
.
如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.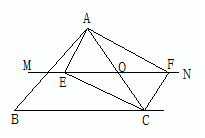
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论
某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.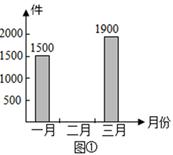
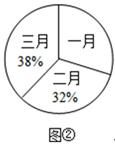
根据上述信息,回答下列问题:
(1)求该厂一月份产量占第一季度总产量的百分比?
(2)该厂第一季度的总产量是多少?并在图①中补完直方图.
(3)该厂质检科从第一季度各月的产品中随机抽样,抽检结果发现样品在一月、二月、三月的合格率分别为95%、97%、98%.请你估计:该厂第一季度大约生产了多少件合格的产品?
已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF=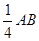 ,猜想EF与DE的位置关系,并说明理由.
,猜想EF与DE的位置关系,并说明理由.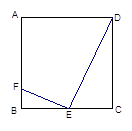
在平行四边形 中,
中,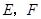 分别为边
分别为边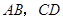 的中点,连接
的中点,连接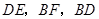 .
.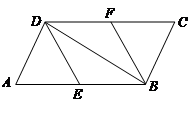
(1)求证: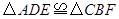 .
.
(2)若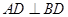 ,则四边形
,则四边形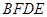 是什么特殊四边形?请证明你的结论.
是什么特殊四边形?请证明你的结论.