(1)如图1,菱形的顶点、在菱形的边上,且,请直接写出的结果(不必写计算过程)
(2)将图1中的菱形绕点旋转一定角度,如图2,求;
(3)把图2中的菱形都换成矩形,如图3,且,此时的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.

如图,已知反比例函数 的图象与直线 相交于点 , .
(1)求出直线 的表达式;
(2)在 轴上有一点 使得 的面积为18,求出点 的坐标.

如图,小莹在数学综合实践活动中,利用所学的数学知识对某小区居民楼 的高度进行测量,先测得居民楼 与 之间的距离 为 ,后站在 点处测得居民楼 的顶端 的仰角为 ,居民楼 的顶端 的仰角为 ,已知居民楼 的高度为 ,小莹的观测点 距地面 .求居民楼 的高度(精确到 .(参考数据: , , .

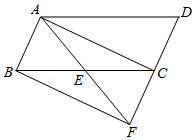
如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.
今年植树节期间,某景观园林公司购进一批成捆的 , 两种树苗,每捆 种树苗比每捆 种树苗多10棵,每捆 种树苗和每捆 种树苗的价格分别是630元和600元,而每棵 种树苗和每棵 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵, 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进 种树苗和 种树苗各多少棵?并求出最低费用.
为了提高学生的综合素养,某校开设了五门手工活动课,按照类别分为: "剪纸"、 "沙画"、 "葫芦雕刻"、 "泥塑"、 "插花".为了了解学生对每种活动课的喜爱情况,随机抽取了部分同学进行调查,将调查结果绘制成如图两幅不完整的统计图.

根据以上信息,回答下列问题:
(1)本次调查的样本容量为 ;统计图中的 , ;
(2)通过计算补全条形统计图;
(3)该校共有2500名学生,请你估计全校喜爱"葫芦雕刻"的学生人数.