如图，抛物线ymx252mx4与x轴交于A(x1，0)，B(-优题课

题文

如图，抛物线 $y = m x^{2} - \frac{5}{2} mx - 4$ 与 $x$ 轴交于 $A (x_{1}$ ， $0)$ ， $B (x_{2}$ ， $0)$ 两点，与 $y$ 轴交于点 $C$ ，且 $x_{2} - x_{1} = \frac{11}{2}$ ．

（1）求抛物线的解析式；

（2）若 $P (x_{3}$ ， $y_{3})$ ， $Q (x_{4}$ ， $y_{4})$ 是抛物线上的两点，当 $a ⩽ x_{3} ⩽ a + 2$ ， $x_{4} ⩾ \frac{9}{2}$ 时，均有 $y_{3} ⩽ y_{4}$ ，求 $a$ 的取值范围；

（3）抛物线上一点 $D (1, - 5)$ ，直线 $BD$ 与 $y$ 轴交于点 $E$ ，动点 $M$ 在线段 $BD$ 上，当 $∠ BDC = ∠ MCE$ 时，求点 $M$ 的坐标．

科目数学题型解答题难度较难

知识点：一次函数的性质解直角三角形待定系数法求二次函数解析式二次函数综合题等腰直角三角形

登录免费查看答案和解析

相关试题

已知:△ABC ∠A=64⁰，角平分线BP、CP相交于点P。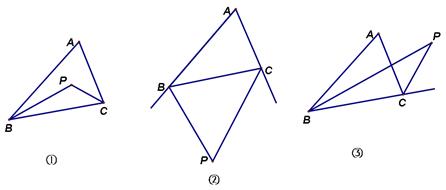

若BP、CP是两内角的平分线，则∠BPC=(直接填数值)
求证: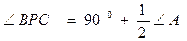
若BP、CP是两外角的平分线，则∠BPC=(直接填数值)
若BP、CP是一内角的平分线，一外角的平分线，则∠BPC=(直接填数值)
由①②③的数值计算可知：∠BPC与∠A有着密切的数量关系，请就第②③写出你的发现

光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台，现将这50台收割机派往A，B两地区收割农作物，其中30台派往A地区，20台派往B地区．两地区与该农机租赁公司商定的每天的租赁价格见下表．

	每台甲型收割机的租金	每台乙型收割机的租金
A地区	1800元	1600元
B地区	1600元	1200元

设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），求y与x之间的函数关系式，并写出x的取值范围；
若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来；

已知函数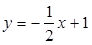和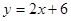
作出这两个一次函数的图象
由图象可知，方程组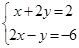的解是多少？
由图象可知,不等式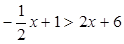的解集是？
如果点P(x,y)的横、纵坐标都是整数，同时符合条件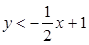、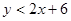且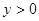，由图象可知，点P的坐标是？

已知:在△ABC中，∠B <∠C, AD平分∠BAC，AE⊥BC，垂足为点E。 ∠B=38⁰,∠C=70⁰。

求∠DAE的度数
试写出∠DAE与∠B、∠C之间的一般等量关系式（只写结论）

通常把一个多边形每一个顶点处的一个外角的和叫做多边形的外角和。试证明三角形的外角和等于360⁰
已知：如图∠1、∠2、∠3是△ABC的三个外角
求证：
证明：

试卷网试题网古诗词网作文网范文网