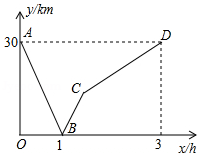
小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离与小王的行驶时间之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少?
(2)求线段所表示的与之间的函数解析式,并写出自变量的取值范围.
(本小题满分9分)我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
(本小题满分9分)为了掌握我市中考模拟数学试题的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为160分)分为5组:第一组85~10;第二组100~115;第三组115~130;第四组130~145;第五组145~160,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图,观察图形的信息,回答下列问题:
(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;
(2)若将得分转化为等级,规定:得分低于100分评为“D”,100~130分评为“C”,130~145分评为“B”,145~160分评为“A”,那么该年级1500名考生中,考试成绩评为“B”的学生大约有多少名?
(3)如果第一组只有一名是女生,第五组只有一名是男生,针对考试成绩情况,命题教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想,请你用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率.
(本小题满分9分)如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
如图,已知抛物线 (
( )与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
)与x轴相交干点A、B.与y轴相交于点C,且点A在点B的左侧.
(1)若抛物经过点C(2,2),求实数m的值;
(2)在(1)的条件下,解答下列问题:
①求出△ABC的面积;
②在抛物线的对称轴上找一点H,使AH+CH最小,并求出点H的坐标;
(3)在第四象限内,抛物线上是否存在点M,使得以点A、B、M为顶点的三角形与△ACB相似?若存在,求m的值;若不存在.请说明理由.
如图,AB是⊙O的弦,D为半径OA的中点.过D作CD⊥OA交弦AB于点E,交⊙O于点F.且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= .求⊙O的半径.
.求⊙O的半径.