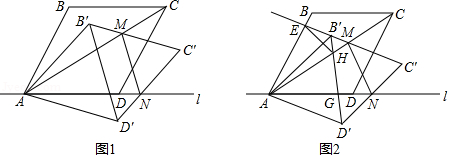
如图1,菱形的顶点,在直线上,,以点为旋转中心将菱形顺时针旋转,得到菱形,交对角线于点,交直线于点,连接.
(1)当时,求的大小.
(2)如图2,对角线交于点,交直线与点,延长交于点,连接.当的周长为2时,求菱形的周长.
(1)已知二次函数y=ax2+bx+c(a≠0)的图象过A(2,0)、B(12,0),且y的最大值为50,求这个二次函数的解析式;
(2)抛物线顶点P(2,1),且过A(-1,10),求抛物线的解析式.[来
已知双曲线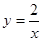 上一点M(1,m)和双曲线
上一点M(1,m)和双曲线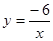 上一点N(n,3).
上一点N(n,3).
(1)求m、n的值;
(2)求△OMN的面积.
在直角坐标系xOy中,已知点P是反比例函数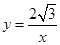 (x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.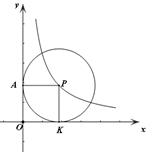
(2)如图2,⊙P运动到与x轴相交,设交点为B,C.当四边形ABCP是菱形时:①求出点A,B,C的坐标;②反比例函数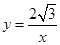 (x>0)图象上是否存在点M,使△MBP的面积是菱形ABCP面积的
(x>0)图象上是否存在点M,使△MBP的面积是菱形ABCP面积的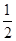 ,若存在,直接写出所有满足条件的M点的坐标;若不存在,试说明理由.
,若存在,直接写出所有满足条件的M点的坐标;若不存在,试说明理由.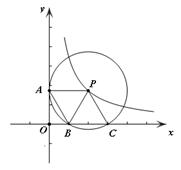
如图,四边形ABCD、BEFG均为正方形.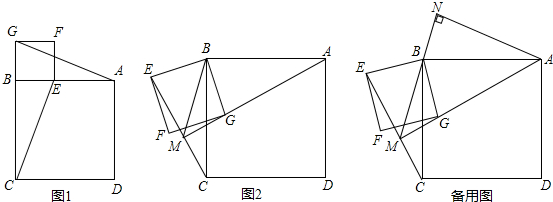
(1)如图1,连接AG、CE,试判断AG和CE的数量关系和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.
(3)在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系.
如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).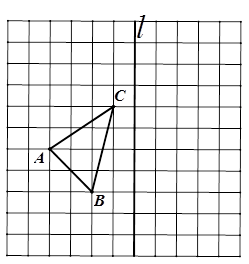
(1)在图中作出△ABC关于直线 对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C;
(3)在⑵的条件下直接写出点B旋转到B2所经过的路径的长.(结果保留π).