十八大以来,某校已举办五届校园艺术节,为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
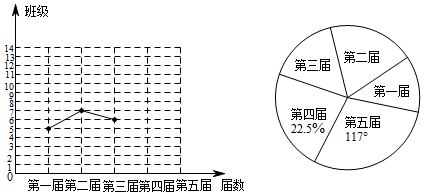
(1)五届艺术节共有 个班级表演这些节目,班数的中位数为 ,在扇形统计图中,第四届班级数的扇形圆心角的度数为 ;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演 “经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用,,,表示),利用树状图或表格求出该班选择和两项的概率.
已知抛物线与y轴交于点C,与x轴交于A(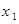 ,0),B(
,0),B(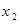 ,0),(
,0),(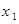 <
<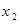 )两点,顶点M的纵坐标为
)两点,顶点M的纵坐标为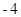 ,若
,若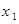 ,
,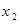 是方程
是方程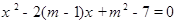 的两根,且
的两根,且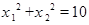 。
。
(1)、求A、B两点的坐标。
(2)、求抛物线的表达式及点C的坐标。
(3)、抛物线上是否存在点P,使△PAB的面积等于四边形ACMB面积的2倍,若存在,求出点P的坐标,若不存在,请说明理由。
关于x的方程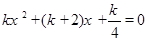 有实数根.
有实数根.
(1)求k的取值范围.
(2)若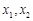 是方程
是方程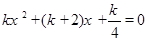 的两个实数根,且满足
的两个实数根,且满足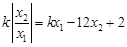 ,求k.
,求k.
列方程解应用题
楚天汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润25万元,那么该月需售出多少辆汽车?(注:销售利润=销售价-进价)
关于x的一元二次方程 有实根.
有实根.
(1)求a的最大整数值;
(2)当a取最大整数值时,①求出该方程的根;②求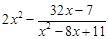 的值.
的值.
如图,抛物线 与x轴交于A,B两点,与直线
与x轴交于A,B两点,与直线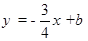 相交于B,C两点,连结A,C两点。
相交于B,C两点,连结A,C两点。
(1)写出直线BC的解析式
(2)求△ABC的面积