如图，顶点为M的抛物线yax2bx3与x轴交于A(1,0)，-优题课

题文

如图，顶点为 $M$ 的抛物线 $y = a x^{2} + bx + 3$ 与 $x$ 轴交于 $A (- 1, 0)$ ， $B$ 两点，与 $y$ 轴交于点 $C$ ，过点 $C$ 作 $CD ⊥ y$ 轴交抛物线于另一点 $D$ ，作 $DE ⊥ x$ 轴，垂足为点 $E$ ，双曲线 $y = \frac{6}{x} (x > 0)$ 经过点 $D$ ，连接 $MD$ ， $BD$ ．

（1）求抛物线的表达式；

（2）点 $N$ ， $F$ 分别是 $x$ 轴， $y$ 轴上的两点，当以 $M$ ， $D$ ， $N$ ， $F$ 为顶点的四边形周长最小时，求出点 $N$ ， $F$ 的坐标；

（3）动点 $P$ 从点 $O$ 出发，以每秒1个单位长度的速度沿 $OC$ 方向运动，运动时间为 $t$ 秒，当 $t$ 为何值时， $∠ BPD$ 的度数最大？（请直接写出结果）

科目数学题型解答题难度较难

知识点：圆周角定理待定系数法求二次函数解析式三角形的外接圆与外心翻折变换（折叠问题）切线的判定二次函数综合题

登录免费查看答案和解析

相关试题

已知抛物线m：y=ax²+bx+c(a ≠ 0) 与x轴交于A、B两点(点A在左)，与y轴交于点C，顶点为M，抛物线上部分点的横坐标与对应的纵坐标如下表：

（1）根据表中的各对对应值，请写出三条与上述抛物线m有关（不能直接出现表中各对对应值）的不同类型的正确结论；
（2）若将抛物线m，绕原点O顺时针旋转180°，试写出旋转后抛物线n的解析式,并在坐标系中画出抛物线m、n的草图；
（3）若抛物线n的顶点为N，与x轴的交点为E、F（点E、 F分别与点A、B对应），试问四边形NFMB是何种特殊四边形？并说明其理由．

如图，在正方形网格图中建立直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：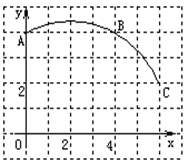

(1) 请在图中确定该圆弧所在圆心D点的位置，D点坐标为______；
(2) 连接AD、CD，求⊙D的半径及扇形ADC的圆心角度数；
(3) 若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径。

如图，已知Rt△ABC和Rt△EBC，°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切，D为切点，AD//BC。

（1）用尺规确定并标出圆心O；（不写做法和证明，保留作图痕迹）
（2）求证：[（3）若AD=1cm，，求BC长。

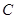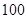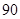在学校组织的“知荣明耻，文明出行”知识竞赛中，每班参加比赛的人数相同，成绩分为、、、四等，其中相应等级的得分依次记为分、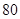分、分、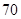分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：

请你根据以上提供的信息解答下列问题：
（1）此次竞赛中二班在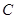级以上（包括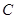级）的人数为；
（2）请你将表格补充完整：

（3）请你从下列不同角度对这次竞赛成绩的结果进行分析：
①从平均分和中位数的角度来比较一班和二班的成绩；②从平均分和众数的角度来比较一班和二班的成绩；③从级以上（包括级）的人数的角度比较一班和二班的成绩．

如图①，在□ABCD中，E在CD上，点C′在AD上，若把△BCE沿BE折叠，点C与C′重合。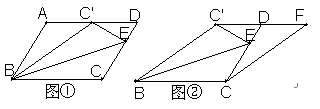

（1）在图①中，请直接写出四对相等的线段；
（2）将图①中的△AB C′剪下拼接在图②中△DCF的位置上（其中△AB C′的三个顶点A、B、 C′分别与△DCF的三个顶点D、C、F重合，且图②的点C′、D、F在同一直线上）试判断图②中的四边形BCF C′的形状并说明理由。

试卷网试题网古诗词网作文网范文网