4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
一、数据收集,从全校随机抽取20学生,进行每周用于课外阅读时间的调查,数据如下(单位:
30 |
60 |
81 |
50 |
44 |
110 |
130 |
146 |
80 |
100 |
60 |
80 |
120 |
140 |
75 |
81 |
10 |
30 |
81 |
92 |
二、整理数据,按如下分段整理样本数据并补全表格:
课外阅读时间 |
||||
等级 |
||||
人数 |
3 |
8 |
三、分析数据,补全下列表格中的统计量:
平均数 |
中位数 |
众数 |
80 |
81 |
四、得出结论:
①表格中的数据: , , ;
②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为 ;
③如果该校现有学生400人,估计等级为“”的学生有 人;
④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读 本课外书.
先化简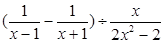 ,然后从
,然后从 ,1,-1中选取一个你认为合适的数作为x的值代入求值.
,1,-1中选取一个你认为合适的数作为x的值代入求值.
计算: .
.
如图,反比例函数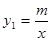 与一次函数
与一次函数 的图像交于两点A(
的图像交于两点A(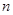 ,-1)、B(1,2).
,-1)、B(1,2).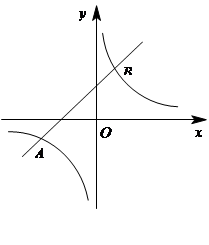
(1)求反比例函数与一次函数的关系式;
(2)根据图象,直接回答:当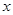 取何值时,
取何值时, ≥
≥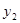 ?
?
(3)连接OA、OB,求△AOB的面积;
(4)在反比例函数的图象上找点P,使△POB为等腰三角形,这样的P点有几个?
并直接写出两个满足条件的点P的坐标.
某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个
工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产
品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付
甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共需付加工费多少元?
码头工人往一艘轮船上装载货物.装完货物所需时间 与装载速度
与装载速度 之间的函数关系如图:
之间的函数关系如图: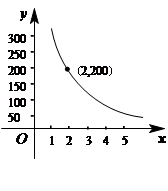
(1)这批货物的质量是多少?
(2)写出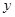 与
与 之间的函数关系式;
之间的函数关系式;
(3)轮船到达目的地后开始卸货,如果要在2小时内
将货物卸完,则卸货速度至少为每分钟多少吨?