文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 |
年龄段 |
频数(人数) |
第1组 |
5 |
|
第2组 |
||
第3组 |
35 |
|
第4组 |
20 |
|
第5组 |
15 |

(1)请直接写出 , ,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有岁的市民300万人,问岁年龄段的关注本次大会的人数约有多少?
某工厂接受一批支援四川省汶川灾区抗震救灾帐蓬的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=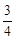 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)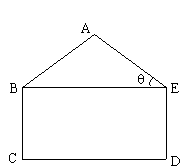
如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标. 
为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.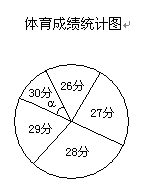
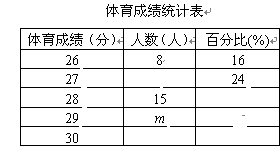
根据上面提供的信息,回答下列问题:
(1)写出样本容量、m的值及抽取部分学生体育成绩的中位数;
(2)已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
先化简,再求值: ,其中x=-4.
,其中x=-4.
计算: .
.